Boxplots

Box-and-whiskers plot

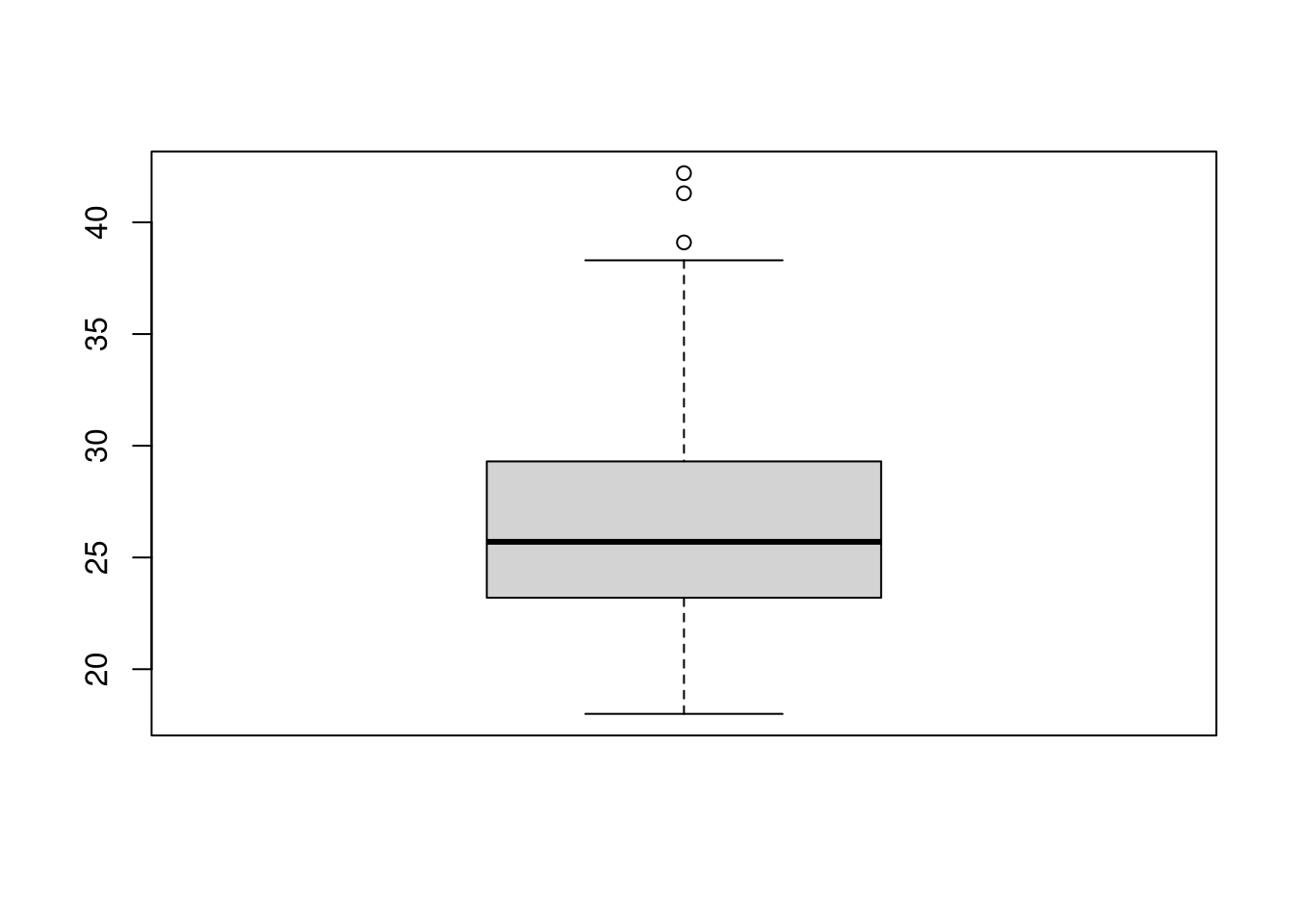
The boxplot (AKA, box-and-whiskers plot) is one of the most enduring contributions of Tukey’s seminal book Exploratory Data Analysis. A boxplot is a visualization of a numeric variable’s so-call “five-number-summary” that quantifies a variable’s distribution through five order statistics: minimum, first quartile, median, third quartile, maximum. Boxplots are particularly useful for evaluating the spread and symmetry of a distribution and checking for extreme values.

Do: Run the code below that uses the boxplot() function to create a boxplot with Base R graphics of BMI from the diabetes dataset.

boxplot(diabetes$bmi)

See: Similar to what we saw with the histogram and density plot, BMI has a long right tail. In a boxplot, we see that as the median falls closer to first quartile than the third quartile, and the upper whisker is longer than the lower whisker.

The “box” part of a box-and-whiskers plot is always defined by first and third quartiles, \(Q_1\) and \(Q_3\), with the median drawn somewhere inside the box. So, this box tells us something about the symmetry and spread of the middle 50% of the distribution.

The “whiskers”, on the other hand, tell us about the tails of the distribution. We can define the whiskers in several different ways to target specific information. In the default boxplot, the whiskers are defined in terms of the inner-quartile range \(\textrm{IQR} = Q_3 - Q_1\).

  • Lower whisker: \(Q_1 - 1.5 \times \textrm{IQR}\)
  • Upper whisker: \(Q_3 + 1.5 \times \textrm{IQR}\)

We can change the weight applied to the IQR via the range argument.

Predict: What will happen to the number of points plotted as individual outliers if we widen the whisker margin from \(1.5 \times \textrm{IQR}\) to \(2 \times \textrm{IQR}\): will more or fewer points fall outside the whiskers?

boxplot(diabetes$bmi,
        range = 2,
        xlab = "Body Mass Index",
        main = "Margin = 3 * IQR")

Explain: Widening the margin pulls the whiskers further out, so fewer points fall outside them and get flagged as individual outliers. Taking this to its logical extreme, we can set range = 0 to use the minimum and maximum values to define the whiskers, meaning no observations get flagged as outliers at all.

boxplot(diabetes$bmi,
        range = 0,
        xlab = "Body Mass Index",
        main = "Min/Max Whiskers")

Boxplots for Outlier Analysis

Any observations that fall outside the interval defined by the whiskers are plotted as individual points. This behavior makes boxplots a handy way to check for extreme values (i.e., outliers). If we set the whiskers so they define the range of plausible values, any points that fall outside the whiskers are possible outliers.

A common convention is to use a margin of \(1.5 \times \textrm{IQR}\) to flag “possible” outliers and a margin of \(3 \times \textrm{IQR}\) to flag “probable” outliers.

Do: Run the code below to use the \(1.5 \times \textrm{IQR}\) for flagging possible outliers.

boxplot(diabetes$bmi,
        range = 1.5,
        xlab = "Body Mass Index",
        main = "Possible Outliers")

See: With the default \(1.5 \times \textrm{IQR}\) margin, several observations fall outside the whiskers and are plotted as individual points flagged as possible outliers.

Predict: Before looking at a boxplot with a wider margin, predict what will happen to the number of flagged points if we widen the whisker margin to \(3 \times \textrm{IQR}\): will more or fewer points be flagged as outliers?

boxplot(diabetes$bmi,
        range = 3,
        xlab = "Body Mass Index",
        main = "Probable Outliers")

Explain: Widening the margin to \(3 \times \textrm{IQR}\) pulls the whiskers further out, so fewer points fall outside them: 3 observations are flagged as possible outliers, compared to only 0 flagged as probable outliers under the wider margin.

Common Mistake

It’s tempting to treat every point flagged by the default \(1.5 \times \textrm{IQR}\) rule as a genuine data error that should be removed. But this rule is just a heuristic convention, not a statistical test for whether an observation is “real” or not. A flagged point might be a legitimate, if unusual, observation. Before removing or downweighting any flagged points, it’s worth checking whether they make substantive sense given what you know about the variable.

Practice exercise

Use the titanic data to create a boxplot of age.

  • Use a margin of \(2 \times \textrm{IQR}\) to define the whiskers.
  • Add a better plot title
  • Add a better label for the x-axis

NOTE: The titanic dataset is already loaded in the working directory of this webr session.

boxplot(titanic$age,
        range = 2,
        xlab = "Age",
        main = "Ages of Titanic Passengers")

Back to top